【学术】 为什么学习测绘要从坐标系出发?
刘克强
我本科的时候学习的是测绘工程专业,但有件事情是我刚进大学学习专业课时最想不明白的,为什么每一本专业书一开始就要“莫名奇妙”地讨论坐标系呢?
先说一点题外话。
我们都知道教育对一个人很重要,无论是从人格的培育,还是从技能的培养角度,接受教育都是会让人提升层次的方法。我觉得接受教育这件事有两个重要方面,一个是接受的内容,另一个是接受的方式,从内容的角度,我们接受的无非都是前人经验知识的积累,而接受的方式也有很多种,而一般情况下我们最主要的受教育的方式就是学校教育。无论是内容还是方式,教育行为都是也还是被人设计的,所以难免有一些缺陷,比如我们的教材和课堂教育方式。拿教材举个例子,很多时候我们是在被动地接受知识的灌输,没有人告诉我们为什么要按照这个途径去学习。比如数学,从小学的算术到初中的几何、代数,再到高中的解析几何、排列组合,以及本科的微积分、线性代数和概率统计等等,这些基本上是按照数学史来的,符合人类文明从发现相关问题,进而解决和提炼数学知识的历史进程,但是,当我们身处其中的时候,“只见树木不见森林”,并没意识到或者想要去了解这个问题,尽管我们在接受学校教育的年龄段去认识这些对数学的学习也不一定会有什么用。
言归正传。
事实上,我觉得我们测绘方面的教材设计上也存在一些问题。大家都知道,很多时候,我们教材方面的书都会设定目标读者,比如一般书籍中提到的“相关学科的本科生或研究生”,也就是说,需要默认你是具备了某些知识背景,但这么做事实上大有逃避铺垫的嫌疑。当然,如果每一本测绘和地理信息方面的书前面加上坐标系的介绍就算铺垫的话,那为什么要这么干或者说坐标系为什么重要就鲜有作者去做解释了。
在谈论坐标系之前,我们先来看看我们的地球。不精确地说,太空中的诸多行星就是一个个“石头”,各个“石头”组成成分不一,形态各异。对地球来说,其表面除了固态的石头之外,还有液态的水。由于外层包裹着大气,在太空中看地球其类似一个椭球体,但是真实的地球表面却“起伏不平”,拥有高山、峡谷、海岸、海沟等等地貌,最高和最低处差距约为两万米。

假设你站在某个历史节点上,你想进行远航,导航定位一定就成了必需品,而导航定位无非就是要说清楚你在哪,想去哪,该怎么去的问题。从最简单的日出日落到北极星,再到指南针,无非都是告诉我们,我们跟起点或终点的相对方位是什么,如果再加上里程,基本上就能确定大致的位置,也就是说,利用方向和距离我们就可以定位和导航。但上述方式粒度太大,如果在陆地上不断地进行修正(如城市、名川大河等),可以找到目的地,但如果在海上,这种基本上就靠运气了。
先不说我们能不能获取高精度的位置,在此之前的问题是,如果要在我们地球这种不规则的石头上精确描述位置,该怎么办?数学史中,坐标系的发明,使得精确描述平面或立体空间成为可能,催生了解析几何,为了在我们地球这种不规则的石头上描述位置,首先需要的工具是参考系统,也就是坐标系。
数学都是从具体问题中找共性,越来越抽象,但我们定位还要面临个实际的问题,那就是地球上怎么建立坐标系呢?首先我们肯定是从上述方位和距离的方式进行延伸:既然地球是个球,那我们就在地表建立个格网,确定原点,然后就可以描述位置了,比如说经纬网、格林尼治零度经线和赤道,这些就构成了我们的地理坐标系。
但是地球又是不规则的椭球,那怎么去构建这个假象的坐标系呢,比如你随便捡起的一个石头,买回来的苹果、梨或西瓜,你想告诉你们家蚂蚁去石头的某个位置,该怎么办?虽然地球是不规则的椭球,但到底还像个椭球,干脆我们找个数学上比较好的椭球去套地球好了。
如果把海水面想象地延伸到地球内部,抹平这些表面上的高山沟壑,是不是就形成了一个椭球球面呢?答案是肯定的,这就是“大地水准面”,但是由于地球质地不均匀导致各处重力场不一致,所以想象出来的大地水准面几何性也不好。既然是想象,干脆找个数学上的标准椭球直接干这件事好了,这就是参考椭球。
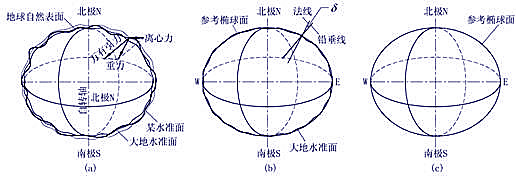
上述坐标系是符合人类认知的,毕竟我们生活在地球表面,也就是椭球表面上的坐标系,但最方便的坐标系应该是笛卡尔坐标系,也就是三轴坐标系。固定一个三轴坐标系就是确定原点和朝向的问题,比如把它放在地球的哪个地方,三个垂直的轴分别朝哪些方向,一般来说原点放在地球的质心,这时如果三个轴向固定好方向,就是确定了坐标系。一般来说地球上的地心惯性坐标系就是这种坐标系,惯性坐标系是相对整个宇宙没有加速度和转动的坐标系,但地心惯性坐标系即使朝向恒星(比如太阳),地球的公转有加速度,而且从整个银河系也是在转动的,所以地心惯性坐标系不是严格的惯性坐标系。尽管宇宙都处在变化当中,地球肯定也处在不断变化之中,但知识是有限定作用范围的,就像牛顿定律适用于宏观低速一样,所以前文建立的惯性坐标系在一定程度上是适用的。
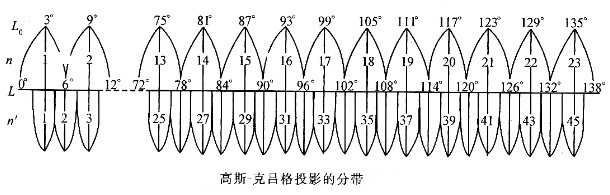
事情到此,好像都挺完满的,但是大家生活中使用的地图都是平面的,如果我们只有三维坐标系,在平时使用的时候该怎么办呢?拥有了三维空间中的位置,我们还需要将三维的球面坐标转换为平面坐标,这里就需要使用地图投影,然而球体是不可能展成平面的,所以投影不可避免的产生变形,变形表现在三个方面,即长度、角度和面积,通常在具体使用中根据需求选择不同的投影方法。我国基本比例尺地形图(1:100万、1:50万、1:25万、1:10万、1:5万、1:2.5万、1:1万、1:5000)除1:100万以外均采用高斯-克吕格Gauss-Kruger投影(横轴等角切圆柱投影,又叫横轴墨卡托Transverse Mercator投影)为地理基础。
为了便于地形图的测量作业,在高斯-克吕格投影带内布置了平面直角坐标系统,具体方法是,规定中央经线为X轴,赤道为Y轴,中央经线与赤道交点为坐标原点,x值在北半球为正,南半球为负,y值在中央经线以东为正,中央经线以西为负。由于我国疆域均在北半球,x值均为正值,为了避免y值出现负值,规定各投影带的坐标纵轴均西移500km,中央经线上原横坐标值由0变为500km。为了方便带间点位的区分,可以在每个点位横坐标y值的百千米位数前加上所在带号。
总结一下,通过建立参考椭球并确定其与地球关系,利用在参考椭球上建立的大地坐标系可以描述地球上的空间位置,除此之外,另一种表示三维空间的坐标系就是直角坐标系,而为了易于平面展示,需要建立平面投影,从而获取了平面地图,而地形图绘制中最重要的平面投影是高斯-克吕格投影。
现在让我们再回到标题的问题,为什么测绘专业课要从坐标系出发呢?测绘就是测量和绘图,测量和绘图地物的位置关系最重要,而想精确描述位置,不得不使用坐标系。